【簡単AI活用】線形回帰を使って未来の売上を予測

【簡単AI活用)】線形回帰を使って未来の売上を予測

グラフのマジック

まず今回は、データを元にグラフを描画し、 測定範囲以上の値を予測したり、途中抜けているデータの値を予測したり、とグラフをベースに作業を進めていきます。そのためグラフの基本的な知識が欠かせません。

例えばエクセルで作成した下記のグラフ、このグラフは傾向を把握するのに正しいグラフと言えるでしょうか？

画像クリックで拡大

答えは No ですね。理由は、元データは店舗数と売上のデータですが、グラフの方は横軸が店舗数ではなく項目のリスト順を示しているだけとなっています。このため店舗数に応じた売上推移を把握することができないグラフとなっています。

横軸の値を変更すれば解決できる問題ですが、オンライン上の Excel では横軸の値を詳しく変更できないため、 Google シートで同じ作業をしてみた結果、店舗数に応じた横軸を示してくれました（下図参照）。

画像クリックで拡大

上図のように最初に Excel で作成したグラフと Google シートで作成したグラフ、特に最初の方はデータ傾向に違いを感じられますね。

こんな風に人工知能や機械学習などを始める際、基本的なグラフの作り方読み方も復習しておく必要があるでしょう。また今後、人工知能や機械学習を Python で扱う場合は、グラフ描画機能の ”matplotlib” も使えると便利。 上記データを matplotlib でグラフ化してみました。

画像クリックで拡大

Pythonでグラフを描くコード

import numpy as np
from matplotlib import pyplot as plt
from matplotlib import style

x,y = np.loadtxt('data.csv', unpack= True, delimiter=',', skiprows=1)

plt.plot(x, y, 'go')
plt.plot(x,y)

plt.title('Sales Graph')
plt.ylabel('Sales(Yen)')
plt.xlabel('Stores')

plt.show()

【コードについて】

import numpy as np
from matplotlib import pyplot as plt
from matplotlib import style

グラフ描画に必要な Pythonライブラリをインポート。 NumPyは、行列や配列データをはじめ、高レベルの数学関数をサポートしてくれるライブラリ。 Matplotlibは、科学技術計算向けのグラフを描いてくれるライブラリ。

x,y = np.loadtxt('data.csv', unpack= True, delimiter=',', skiprows=1)

NumPyのloadtxt()メソッドで元データがある data.csv ファイルを読み込み、skiprow で最初の行を飛ばします。 最初の行は文字列が格納されているため、「消す」か「飛ばす」かしないと loadtxt() できません。 今回は 2列のデータなので x, y 。data.csv 内の 1列目 store を x に、 2列目の sales を y に格納します。

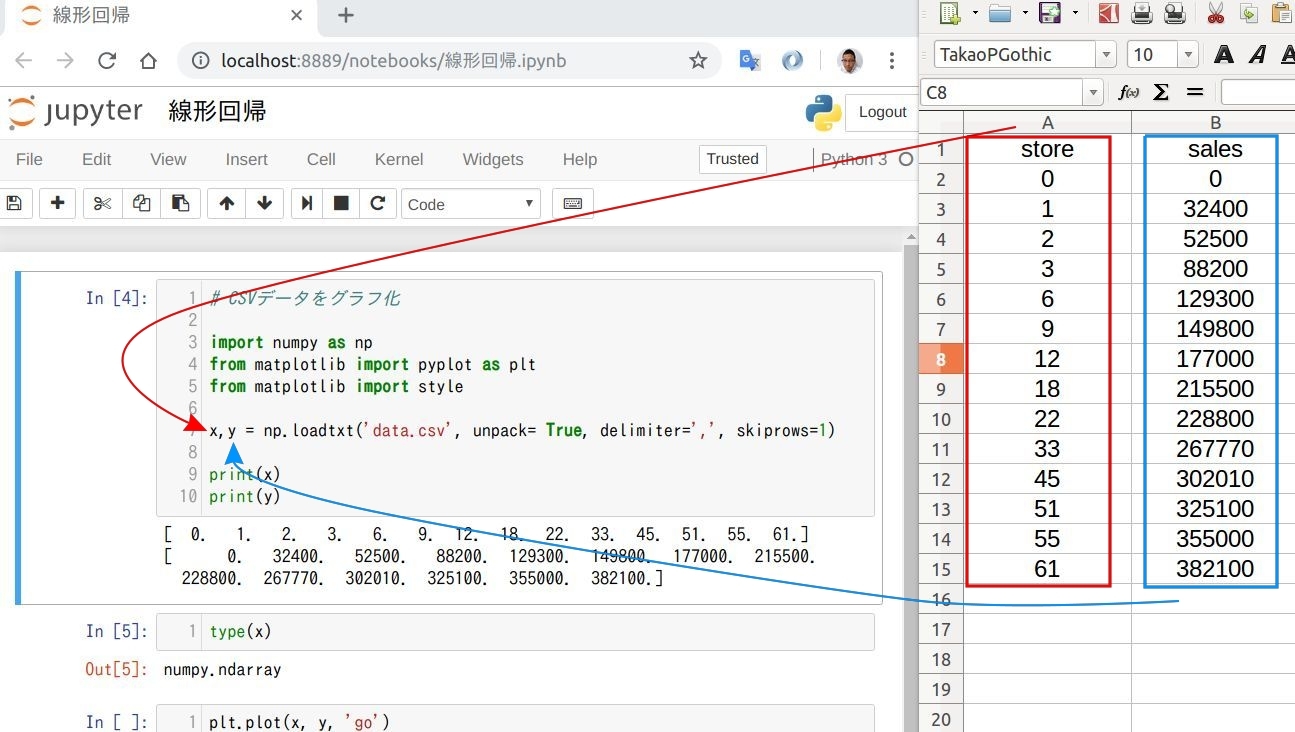
3列ある場合は z などを用意して CSV ファイルのデータを格納します。 csv.reader()メソッドで CSVファイル内のデータを読み込むこともできますが、この場合は”リスト型”データとして読み込まれます。今回は Matplotlib で描画処理しますので、NumPy で読み込む必要があるというわけですね。

plt.plot(x, y, 'go')
plt.plot(x,y)

plt.plot()メソッドで x と y のデータをグラフ上にプロットしてくれます。 'go' と付けるとドットタイプ、何もない場合はラインでグラフ描画。

plt.title('Sales Graph')
plt.ylabel('Sales(Yen)')
plt.xlabel('Stores')

こちらはグラフに表示するタイトルや軸名など。

plt.show()

plt.show() でグラフがモニター上に表示されます。

エクセルに比べ matplotlib はデータをあらかじめ用意しなくても、プログラムコードで数式や関数をグラフ化してくれるので便利。初めての方はコードも matplotlib も扱いにくいかもしれませんが、何度か見るうちに徐々に慣れてくると思います。

次は元データをグラフ化した時、どういう場合に線形回帰が使えるのか確認してみましょう。

線形回帰が使えそうなグラフ

画像クリックで拡大

緑：元データ　　青：線形回帰後のデータ

【線形回帰とは】

線形回帰は、機械学習アルゴリズムの中でも比較的単純で古典的な手法の一つ。 端的にイメージで理解しようと思うと、下図のように X-Y 上に散りばめられたデータの中央値を描写する事ができる機能。 概ねの中央値を難しい数式ではじき出して、予測してくれる機能が「線形回帰」になります。 尚、線形回帰は 一次関数の直線的なデータに対しては有効ですが、曲線的にデータ変化する二次元のデータに対しては誤差が。そうした曲線的なデータに対しては「多項式回帰」が有効です。

線形回帰は散らばったデータの中央値を演算するアルゴリズムなので、処理結果は直線的。そのため上図左のような 一次関数的なデータに対しては、比較的高い精度の予測値を返すことができます。

しかし、上図右のような曲線的なデータに対しては、線形回帰青線を行うことで、横軸の初期地付近はマイナスの値に。 このように2次関数や3次関数的な曲線を描くデータの場合は、多項式回帰を使用しないと正確な予測値をすることはできません。

つまり、高精度の予測値を得るためには、元データをグラフ化して、線形回帰で正しく処理できるかどうか判断しておく必要がありますね。

線形回帰をPythonで行ってみる

数学の公式で線形回帰を行おうと思うと難しいですが、 Python で線形回帰を行うと、難しい数式のことを知らなくても処理できてしまいます。

ただし Python で線形回帰を行う場合、使用するデータを適切な形にセットしておく必要が。最初のうちは分かりにくいデータセットですが、3、4回自分でプログラムを実行してみると要領はつかめると思いますよ。

それでは今回は、当記事冒頭グラフで紹介した 「お店の店舗数と売上に関するデータ」 を用いて 『線形回帰』 を行ってみたいと思います。

データの読み込み

画像クリックで拡大

import numpy as np
import pandas as pd

dataset = pd.read_csv('data.csv')

x = dataset.iloc[:, 0:1].values
y = dataset.iloc[:, 1].values

print(x)
print(y)

今回利用するデータは、店舗数と売上の2列のデータになります。 一列目のデータ（店舗数）を x、 ニ列目のデータ（売上）を y に格納。 iloc はデータの抽出範囲を指定する機能で、 [ : , 0] で 店舗数（store） の列を抽出。[ : , 0:1] とすることで、データを 2次元配列に。 データ x については、 1次元配列では線形回帰処理できず、 2次元配列でデータ管理する必要がありますね。 y については、 一次元で OK なので [ : , 1] に。

実際に x と y をプリントアウトしてみると、読み込まれた内容が確認できると思います（上図参照）。

訓練データとテストデータ

画像クリックで拡大

from sklearn.model_selection import train_test_split

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.3, random_state = 0)
print(x_train)
print(x_test)

線形回帰処理に使うデータ（訓練データ）とテストデータを仕分け、訓練に 7割、テストに 3割と設定。test_size = 0.3 がテストデータの割合で、 0.2 や 0.4 と色々変えてみると面白いと思います。

Excel でデータを分けようと思うとちょっと面倒くさいですが、 sklearn（scikit-learn） を使うと一行のコードで x と y のデータを訓練用とテスト用、計 4種類のデータに分けることが可能。どんな風にデータが分けられた方は、 print() 処理してみるとよく解ると思います（上図では データ x の仕分け状況を確認）。

線形回帰（機械学習）

画像クリックで拡大

from sklearn.linear_model import LinearRegression
regressor = LinearRegression()
regressor.fit(x_train,y_train)

こちらでは訓練用データを用いて線形回帰を実施します。 線形回帰、数式で処理しようと思うと Σ などが出てきて難しいですが、 Python においては sklearn（scikit-learn） の LinearRegression() 関数を使うだけで OK。 fit() 関数で線形回帰の計算（機械学習）を行ってくれます。

テスト

画像クリックで拡大

y_pred = regressor.predict(x_test)
print(x_test)
print(y_pred)

線形回帰の予測値を得ようと思うと、 上図のように predict() 関数を利用すれば OK。 print() でテスト用データ（x_test）と予測値（y_pred） を出力。ただ数値の出力では、ちょっとイケているのかどうか、分かりませんよね。データの推移をグラフ化してみましょう。

線形回帰データをグラフ化

画像クリックで拡大

from matplotlib import pyplot as plt
from matplotlib import style

plt.scatter(x, y, color = 'green')
plt.plot(x, y, color = 'green')

plt.scatter(x_test, regressor.predict(x_test), color = 'blue')
plt.plot(x_test, regressor.predict(x_test), color = 'blue')

plt.title('Sales Graph')
plt.ylabel('Sales(Yen)')
plt.xlabel('Stores')
plt.show()

Matplotlib を使ってデータを可視化、緑線が元データで、青線が線形回帰したデータ。 Store 20 付近は乖離が大きいようにも見えますが、 40 以降はいい感じに見えます。

予測値を取得する

画像クリックで拡大

y_pred = regressor.predict([[100]])
print(y_pred)

せっかく線形回帰を行ったので、未来の値、 100店舗目の売上を予測してもらいましょう。上記コードを実行した結果、 617982円 という結果が。面白いですね。

せっかくなので Web からもこの予測システムを使用できるようにしてみましょう。

Webからでも予測値を取得できるようにしてみる

画像クリックで拡大

予測値の取得は y_pred = regressor.predict([[入力値]]) で行いました。つまり HTML から 入力値にデータをポストし、演算後の結果をゲットできれば Web 上からでも予測値をゲットできそう。

今回は Python の Webフレームワーク Flask を使って実装してみたいと思います。とはいいましても、 一から作っていくのは大変。テンプレートを利用させて頂きます。

Flaskテンプレートの構造

画像クリックで拡大

【コード／GitHub】

api.py に 線形回帰を行ったデータ model.pkl をセットし、 app.py で Webサーバー起動。 Webサーバーが起動すると、 input.html が起動し、データが入力・ポストされれば、入力値に合った予測値が出力されて、 output.html で表示、という流れ。

まだ model.pkl がありませんので、下記コードで model.pkl を作成。

画像クリックで拡大

y_pred = regressor.predict(x_test)
pickle.dump(regressor, open('model.pkl','wb'))
model = pickle.load(open('model.pkl','rb'))

今度は y_pred = regressor.predict([[入力値]]) で予測値を得るのではなく、 print(model.predict([[25]])) で予測値をゲット。 Flask のテンプレート・フォルダに model.pkl をセットして、 Flask を起動してみましょう（下動画参照）。

http://0.0.0.0:5000 を開いて Flask が起動していれば OK。 ただし、 Windows の場合は 0.0.0.0 を消すか、 127.0.0.1 、 localhost などに変更する必要があるでしょう。

線形回帰の様子を紹介する動画

本テキストと合わせてご参照下さい。

まとめ

「えっ、これで人工知能？ 機械学習？」 と思われるかもしれませんが、列記とした機械学習アルゴリズムの線形回帰を使って、データを予測させています。

はじめの内は「機械学習」、というと何だか難しい処理を行うようなイメージはありますが、今回の線形回帰については基本 LinearRegression() と fit() 、 predict() で処理。自分でもプログラムを実行して、数値を変えて色々テストしてみましょう。

「そもそも自分のパソコンで Python できない」「機械学習、興味あるけどサッパリ分からない」という方、思い切ってプログラミングスクールを検討してみませんか？

今後 2、3 年の内に小学校でも AI教育がはじまり、今後益々 AI や機械学習は社会の常識に。モタモタしていては商機を失いますので、考え込んだり、一人で頑張り過ぎる前に、まずは学習効率が大事かもしれませんね。

オンライン型のプログラミングスクール CodeCamp では、無料体験も随時実施しています。 公式ページ よりご確認ください。